《万物皆数》-完-4.5

这本书精装，200多页，分了17章，暂计划一周读完吧，看上去没那么难读。这是一本讲数学简史的书。

临近这本书的尾声，看到第17章，对数学的底层是否稳当可靠有了一种不安感，不可自证，不可判定，悖论……如果有一天底层数学崩塌了，由此而来的物理也废墟了……一代一代人，最聪明的人，不就是忙活着给自己解闷了。但除了相信这些公理以及衍生出来的定理，还能信什么呢。

古巴比伦学者，美索不达米亚人创造无与伦比先进知识，他们3懂得四种基本运算法则——加减乘除，还懂得平方根、乘方和倒数。发展出非常全面的运算表格，甚至还列出方程。

古巴比伦人之后，玛雅人也发明位置记数系统，20进制；古印度发明十进制技术方法。

中国汉朝刘徽伟大数学著作《九章算术》。勾股定理。首先描述了性质与负数类似的数字。

艾拉托斯特尼，古希腊学者测量地球周长。

泰阿泰德，公元前4世纪古希腊数学家，一般认为，他第一个完整描述正多面体。他说只存在5种（四、六、八、十二、二十面体），后来称这5种多面体为“柏拉图立体”。
——关于正多面体的古希腊的故事，最近更多看到的是毕达哥拉斯对正多面体的执着。

“原来病毒在自然情况下呈现正二十面体或正十二面体的形状。病毒的包膜仅有几种不同类型分子构成，彼此配合相嵌，呈现出相同的规律。简洁，经济。”
——原来病毒小得这么完美呢。

泰勒斯，公元前7世纪末，古希腊第一位伟大数学家，“漫不经心学术派”祖师爷。第一个准确预测日食的人。使用几何方法“阴影测量法”测高度。得出数学结论：一个圆任意直径将该圆分成等面积两部分；等腰三角形两个底角相等；任意两条相交线，对顶角度数相等；如果一个三角形的三个定点落在一个圆周上，并且其中一条穿过圆心，这个三角形必然是直角三角形（泰勒斯定理）。

定理，古希腊人表述的名字。数学真理用简洁又概括的方式表达，无论对于所包含的哪一个个别情况，都成立。

泰勒斯在米利都有两个最著名的弟子：阿那克西美尼，阿那克西曼德。阿那克西曼德的知名弟子毕达哥拉斯。
毕达哥拉斯定理，勾股定理。

欧几里得，公元前3世纪，13卷《几何原本》讨论几何学和算术问题。最先采用公理化的方法。人类历史上再版次数第二多著作。

定义-公理-定理-证明，由欧几里得开辟的道路。
悖论，似假非真，似是而非，自相矛盾的命题。挑战了预设，或者真，或者假，没有第三种可能的“排中律”。
公元前5世纪古希腊哲学家芝诺，制造悖论大师，最有名“阿喀琉斯追乌龟”。
目前所有人们想要寻找的数列，都在π中找到了。

阿基米德（古希腊），发明家，解题者，发现杠杆原理。发现阿基米德浮力原理。发明反射镜系统。在测算π值上第一个伟大进步，正多边形切割圆。

丢番图，《算术》。丢番图方程。
克罗狄斯·托勒密，《天文学大成》，囊括了当时人们对天文学和数学的认知。认为太阳绕着地球转。
西帕提娅，女性学者。亚历山大博物馆最后一位学者，被基督徒谋害。

婆罗摩笈多，公元7世纪印度，发表《婆罗摩修正体系》，第一个对数字零和负数，以及它们算术性质完整描述。第一个将零作为一个数字进行完整描述的人，同时描述了数字零的性质。

——对中国人来说，提及东方，首先同时大多也是唯一能想到的国家是自己的国家。对世界而言，提及东方，其实包含了更多的可能，比如另外一个大国——印度。作为几大古国之一的古印度，对人类文明的贡献也是不容小觑的。我们既不了解古印度，也不了解现在的印度。那种刻板印象，可能跟欧美人对我们的印象一样，停留在某个特定的时代，至少得有100年以上吧。印度的阿三？《生活大爆炸》里的印度后裔？比我们贫穷，环境污染，民风刻薄，性别歧视，种姓歧视……然后关于印度的真实、文明，正向的印象就全无了。除了印度教、佛教起源，也并不知道更多。

希腊人是人类历史上第一个建立三角函数表的民族。托勒密的《天文学大成》。

默罕默德·伊本·花拉子米（阿拉伯学者），撰写了著名的《印度数字算术》，将来自印度的十进制推广到全世界。受哈里发马蒙之令，撰写一本给人民学习的数学指南，解决生活问题。他完成了《还原与对消计算概要》，书中介绍了他纯理论研究的一部分，使用了结构性和抽象的写法。后称为代数学。花拉子米开创了新方法设计表达方式。将数学发展趋向于抽象性和普遍性，从现实事物中脱离并独立存在。几何方法求解。花拉子米著作用阿拉伯语写成，一个符号都没有，后来将花拉子米的论证称为“代数修辞”。
代数学的目标，是提出方法来解决这种纯数学的“谜题”。几个世纪后，命名为“方程式”。

阿布·卡米勒（埃及），方程组，若干未知数方程求解。

斐波那契（意大利），《计算之书》介绍了当时所有数学知识。斐波那列数列：1，1，2，3，5，8，13，21，34，55，89，144……
后一个数是前一个数接近φ倍。越来越接近黄金分割。
叶序学：研究组成植物的树叶或者其他不同元素如何围绕着植物轴心旋转生长的学科。

黄金分割，φ（fai）=1.618，古希腊认为完美比例。第一次通过文字被明确界定是在欧几里得《几何原本》。黄金分割率的平方等于黄金分割率+1。花拉子米的方法得出黄金分割精确表达式。φ=（1+5^）/2。

米兰卡尔达诺，发表《大术》，三次方程解析式以他命名，被称为“卡当公式”。但首位解出三次方程的人是意大利的希皮奥内·德尔·费罗，后威尼斯数学家尼科洛·塔尔塔利亚发现解析式，第一个在计算中使用括号符号。卡尔达诺从塔尔塔尼亚交易获得解析式（诗），违背诺言对外发表。

博洛尼亚数学家拉斐尔·邦贝利，发表《代数学》，指出“复杂的数”的平方是负数。两世纪后，笛卡尔赋名：虚数。

“数学家探索理论标准：其一，这个理论必须要有用；其二，这个理论必须是美的。“除非”对于数学来说是不美的，“例外”让人心痛。一则声明越简单、它所指的范围越大，我们就越觉得自己碰触到了某些深刻的东西。”

代数基本定理：一个方程的解的数量等于它的次数。

伽罗瓦，创造新的代数结构，命名“伽罗瓦群”。他证明了从5次方程开始，某些方程的解不可能通过花拉子米公式或卡当公式之类只含四则运算，求幂和求根公式计算。

德国数学家埃米·诺特，抽象代数。

1450年德国人约翰内斯·谷登堡活字印刷传播新观念。1543年波兰天文学家哥白尼发表《天体运行论》，宣称地球绕着太阳转，否定托勒密。后有布鲁诺、开普勒、伽利略，日心说成为新的宇宙参考模型。

法国数学家韦达，新型代数学的主要引导者，出版《分析方法入门》。发起庞大的“代数现代化”计划，用字母表示运算。

法国笛卡尔提议用字母前几个abc表示已知数，最后几个xyz表示未知数。创造简单强大的带有坐标轴和坐标的系统，将几何问题代数化。

“化圆为方”，换成如下：找到一系列一次方程或二次方程，使π成为解。后德国数学家费迪南德·冯7·林德曼终结，数字π不是任何一次方程或二次方程的解，因此化圆为方不可能。

伽利略，意大利科学家。发明天文望远镜，发现土星环，太阳黑子，金星周期，木星四个主要卫星，哥白尼日心说倡导者，阐释物体相对运动。“伽利略变换”描述相对运动的规则。第一个实验研究自由落体运动的人。
“E pur si muove！”——然而，地球是围着太阳转的！

牛顿，英国学者。《自然哲学的数学原理》，地球上自由落体和天空中天体圆周运动，都可以通过同一个现象解释。宇宙中所有物体都相互吸引。精确算出相互吸引两个物体之间引力大小。任意两个质点由通过连心线方向上的力相互吸引，该吸引力的大小与它们质量乘积成正比，与距离平方成反比。牛顿计算出哈雷彗星回归周期。
韦达对其书面化：F=G✖️m₁✖️m₂/d²
F引力强度；m质量；d距离；G=0.0000000000667（6.67✖️10^-11）

1919年5月29日日食，见证爱因斯坦广义相对论的胜利。
2012年希格斯玻色子发现，见证早先预设中粒子物理学标准模型。
2015年9月14日，引力波存在首次被检测到。

天文单位对应地球和太阳之间的距离，大约1.5亿千米。

斯特凡·巴拿赫和阿尔弗雷德·塔斯基悖论。豌豆切割无穷小，重构出太阳那么大球体，且中间不留任何空隙孔洞，有悖常识，但这并不是一个悖论，而是真正定理。“粉状”图形使其成为可能。

瑞士数学家，雅各布·伯努力撰写《猜度术》，提出概率论基本原则之一：大数定律——在随机试验中，重复次数越多，结果平均值越明显（不再是随机的），并且趋近于一个极限值。

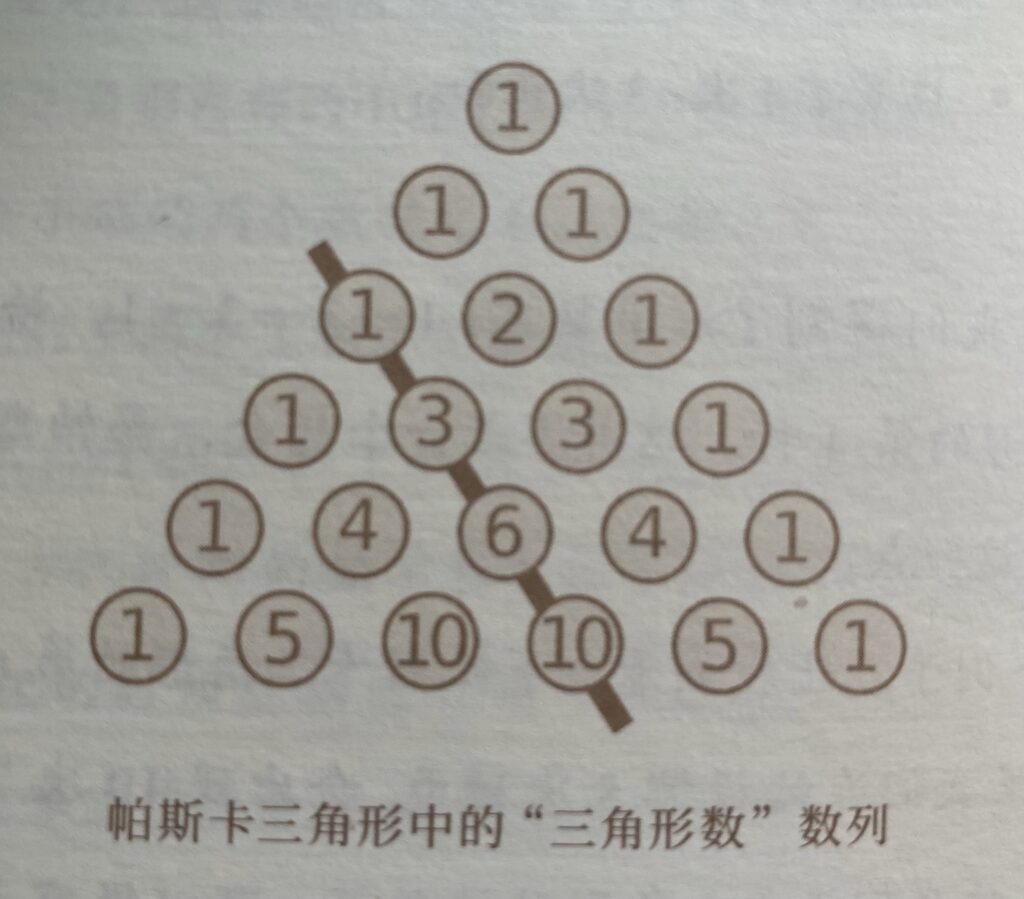
帕斯卡三角形：三角形中，小球上面数字大小由两个规则决定：位于三角形边缘的所有小球，数值都是1；其次，三角形内部小球，每个小球数值等于上面一行中挨着这个小球的两个数值之和。
可找到斐波那契数列。

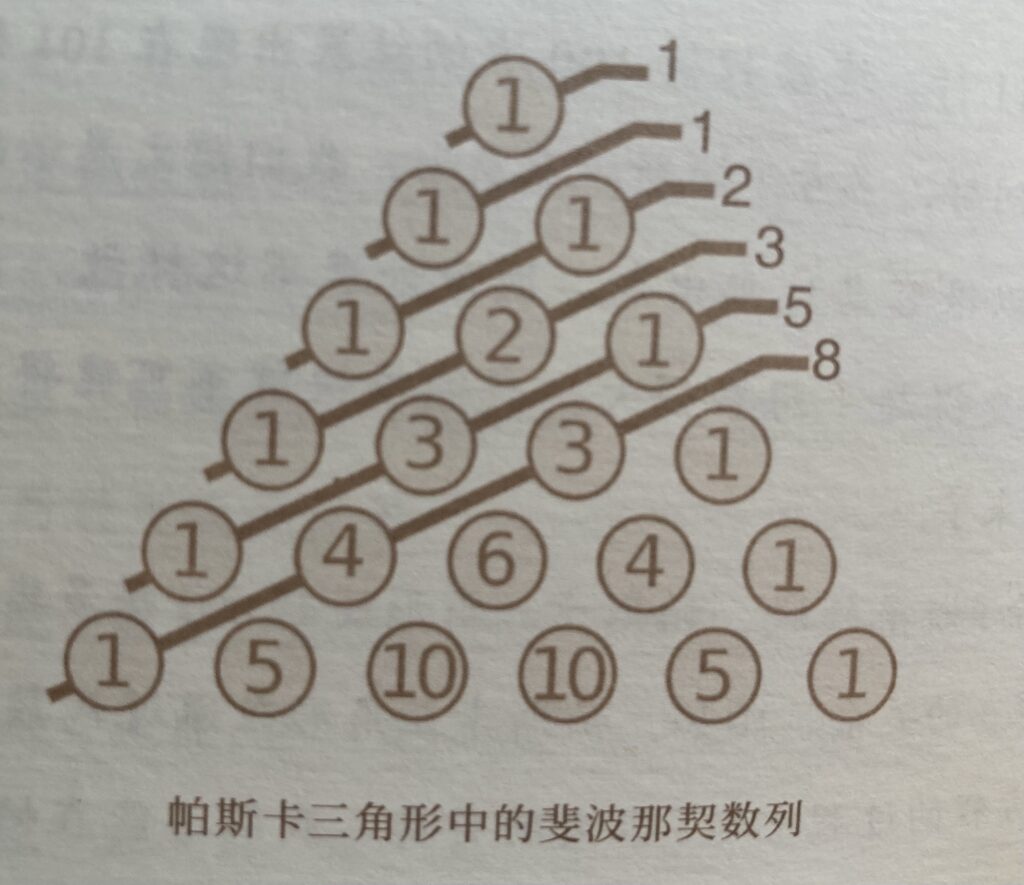
帕斯卡计算器是历史上第一台计算器。

获得某个结果而给计算机下的一系列指令被称为“算法”，来自花拉子米名字的拉丁语变形。

1897年8月8日，瑞士举办第一届国际数学家大会，第二届1900年后续4年一度。发起者德国学者格奥尔格·康托尔（发现“有一些无穷大比别的无穷大更大”，创建集合论）和菲利克斯·克莱因（代数结构方面专家）。200位与会者，来自意大利朱塞佩·皮亚诺（定义现代数论公理）；俄罗斯安德雷·马尔可夫（研究概率论带来颠覆性改变）；法国昂利·庞加莱（混沌理论，“蝴蝶效应”，被有些人认为是“最后一位全知全能伟大学者”，掌握自己时代所有数学知识，在他之后“数学通才”不再，而是“数学专才”）。大会三天。

德国数学家戴维·希尔伯特，20世纪初最具有智慧和影响力数学家，列出人类尚未解决数学难题清单，23个问题。截至2016年，还有4个问题没答案。希尔伯特，实施庞大计划，打造一个独特理论，涵盖所有数学分支，eg笛卡尔坐标，将几何问题用代数语言表述。“超级理论”借助了格奥尔格·康托尔“集合论”框架。1910～1913年，英国数学家阿尔弗雷德·诺思·怀特黑德和伯特兰·罗素出版《数学原理》，最终给出一个定理：1+1=2. 当今，绝大部分现代数学学科确实能够在以结合论为基础若干公理之内，找到学科基础。但1931年，该计划中止——库尔特·哥德尔的不完备定理（找到一种使用数学语言书写元数学命题的方式）。

理论完美，必须满足：一致性（不允许悖论）和完整性（足够证明框架下所有真命题）。

自1936年，每届大会颁发菲尔兹奖，数学界的诺贝尔奖。奖牌上刻有阿基米德浮雕像，一句对这位古希腊数学家的评价：Transire suum pectus mundoque potiri（超越他的心灵，掌握世界）。
目前世界范围内，数学界每4年将会产生大约100万条新定理。

法国数学家本华·曼徳博，曼徳博集合。

数学影像：https://images.math.cnrs.fr/?lang=fr