《混沌与均衡纵横谈》-完-4.1

作者: 梁美灵 / 王则柯
出版社: 大连理工大学出版社
出版年: 2008-4
页数: 270
定价: 24.00元
丛书: 数学科学文化理念传播丛书
ISBN: 9787561140819
简介
围绕混沌理论和经济均衡理论计算方法,着重介绍了李天岩、约克、梅、斯卡夫、菲根鲍姆、斯梅尔等学者近年来在科学上所作的贡献。与一些读者头脑里的老夫子、老学究的形象不同,这些学者全都是极富个性的人物,他们的共同特点是基础深厚,兴趣产泛,对新发展富有远见。他们不是死守一块阵地,而是为开拓不惜改弦更张,一旦认准了目标,他们锲而不舍,务克全功,决不半途而废。这一切,都是科研工作者的可贵品格,都是新科学、新时代探索者的可贵品格。
2024.02.18
这本书从图书馆借来一个月了,特意找的这本书来读,竟然没看,随便摸的两本反倒是读完了。昨天从读书馆里做了续借。今天说什么也要读一读,不能再拖黄了。这本书是讲什么的,早不知了,还是《一生自在》书中提及的。但愿我能读得懂。以后的读书,至少可以加个内容简介了,之前没关注过,是因为不知道这本讲啥所以才copy文字过来,可以形成惯例。
从某个值开始,不断地由上一步的结果计算(或推断)出下一步的结果,就叫迭代算法。eg y=15x(1-x)/4
一 数学:周期三则乱七八糟:讨论[0,1]区间到[0,1]区间的迭代。结论:有一个3周期点的话,那么它有一切周期点。如果xn=f(xn-1)有一个3周期的点的话,那么随便一个正整数k,xn=f(xn-1)这个迭代一定有一个周期为k的点,但迭代次数少于k的话,都不回到原来的地方。
周期点:
y=f(x),f表示因循变化的关系。y随x的变化而变化。x1=f(x0); x2=f(x1); x3=f(x2),……xn=f(xn-1),n=1,2,3……,利用函数关系y=f(x),算出一个y作为新的x再算下一个y的做法,数学上称为迭代。下面简称的区间迭代,都是从[0,1]区间到[0,1]区间的迭代。eg. f(x)=-2x3+1.5x+0.5 那么xn=f(xn-1),n=1,2,3……就是[0,1]区间到[0,1]区间的迭代。
x=0, x’=0.5
x=0.25, x’=0.844
x=0.5, x’=1
x=0.75, x’=0.781
x=1, x’=0
把x放到式子里迭代,得到x‘=f(x),一般来说x’和x会不同,当x’=x,这样的x叫作迭代函数f(x)的不动点,即x*=f(x*),就称x*是f(x)的不动点。[0,1]区间到[0,1]区间的迭代,一定有不动点。
0->0.5->1->0->0.5->1->0->……0叫作f(x)的周期点,0经过3次迭代,又回到0,所以0叫作f(x)的一个3周期点。如果从x0开始按照公式xn=f(xn-1)迭代,经过一定次数迭代后回到x0这个地方,x0叫作f(x)的周期点。
从数学上讲,一个迭代公式反映一个动力系统。点由于迭代而产生的变化和发展情况是动力系统研究的主要对象。只要系统中有一个迭代3次才回到原处的点,这个系统一定非常复杂。研究混乱现象的理论——混沌学(chaos)。
沙可夫斯基定理:沙可夫斯基证明,如果在沙可夫斯基次序中m在n的前面,那么有m周期点的话,一定有n周期点。3在所有自然数前面,如果某个具体的区间迭代有一个周期是3的点的话,它就一定有周期是任意自然数的点。只要有3周期点,就乱七八糟什么周期点都会出现。周期3意味着麻烦。
如果迭代公式xn=f(xn-1)有3周期点,那么它就有一切周期点。

a由一个n周期点按照上面两个图所说的方式产生的一组n个n周期点都是互不相同的点,它们之间没有重叠。
b对于同一个自然数n,两组不同的n周期点也不会重叠。
c如果m和n是两个不同的自然熟,那么m周期点和n周期点一定不会重叠。没有一个点可以既是m周期点,又是n周期点。
3周期间都是3个3个的出现的,5周期点都是五5个5个的出现的,n周期点都是n个n个地出现的,而且它们互不重复,既没有重叠。
单值性:函数f(x)或迭代公式xn=f(xn-1)的单值性指的是:送进去一个x,就算出一个f(x)值;送进去一个xn-1,就算出一个xn值。
设f(x)是[0,1]区间到[0,1]区间的一个连续函数,如果迭代xn=f(xn-1)具有以下性质,就说它有混沌现象:
①迭代xn=f(xn-1)的周期点的周期无上限;(每一个自然数都是有限的,但一切自然数的总体都是无上限的)
②区间[0,1]有一个“不可数”子集S,使得:
– 对于S中任意不同的两点x0和y0,考虑迭代序列xn=f(xn-1)和yn=f(yn-1),n=1,2,3,……,当n趋于无穷大时,它们之间的距离|xn-yn|的上极限大于0,下极限等于0;
– 设y0是迭代的任意一个周期点而x0是S中的任意一点,考虑迭代序列xn=f(xn-1)和yn=f(yn-1),n=1,2,3,……,当n趋于无穷大时,它们之间的距离|xn-yn|的上极限大于0
这一章的后半部分解说,我真的有些看不懂,而且也看不下去。
二 生物:生物科学和医学中的混沌理论
罗伯特·梅(1936-)原物理学家,理论物理和应用数学。1972年,投身生物科学。混沌生物学家。
生物数学家企图把生物系统纳入确定性的系统框架。但一次次失败。
长期共存的两个物种的平均个体重量之比应当是2的倍数。如果差别太小,两个物种是无法长期共存的。平均身长应当是1.3的倍数。
把每个物种的个体数目或总量叫做这个物种的规模。生态学的一个基本问题是从量的方面探讨系统中各物种的自然规模。制约物种的增长能力的环境因素和生物学因素是什么,特别是找出长期起作用的因素。
罗伯特·梅,生态学角度的迭代公式:xn+1=Axn(1-xn),表达某个物种的规模变化规律。这个物种一代一代之间是不交叠的。这种的规模是离散的。xn是该物种第n代的密度;xn+1是该物种第n+1代的密度,A是一个常数。密度总可以表示成一个小于1的正数,无单位的纯量。
当1<A<3,物种的密度经过一代一代的发展,总是趋向于一个稳定值。图a
当3<A<3.570时,物种密度变化发展都呈现周期性质,当A比3大一点时,周期为2,随着A的增大,周期出现4,8,16,32……的变化。图bc
当A>3.570时,构成杂乱无章踪迹,混沌。图d
比3.570大,比4小的A,都会出现混沌,当A>4时,迭代结果趋向负无穷。所以限于讨论0<A<4之间的情形。
1<A<3稳定解;3<A<3.570周期解;3.570<A<4噪音型混沌解。
三 物理:菲根鲍姆常数
菲根鲍姆,美国康奈尔大学物理学家。20世纪重大发现之一:对截然不同的函数进行迭代,在迭代过程转向混沌时,它们竟遵循着同样的规律,受到同一个数字的支配——4.6692
周期倍增分叉现象
菲根鲍姆洞悉了周期倍增分叉现象的更深刻的规律,揭示出系统从有序转向混沌的秘密。
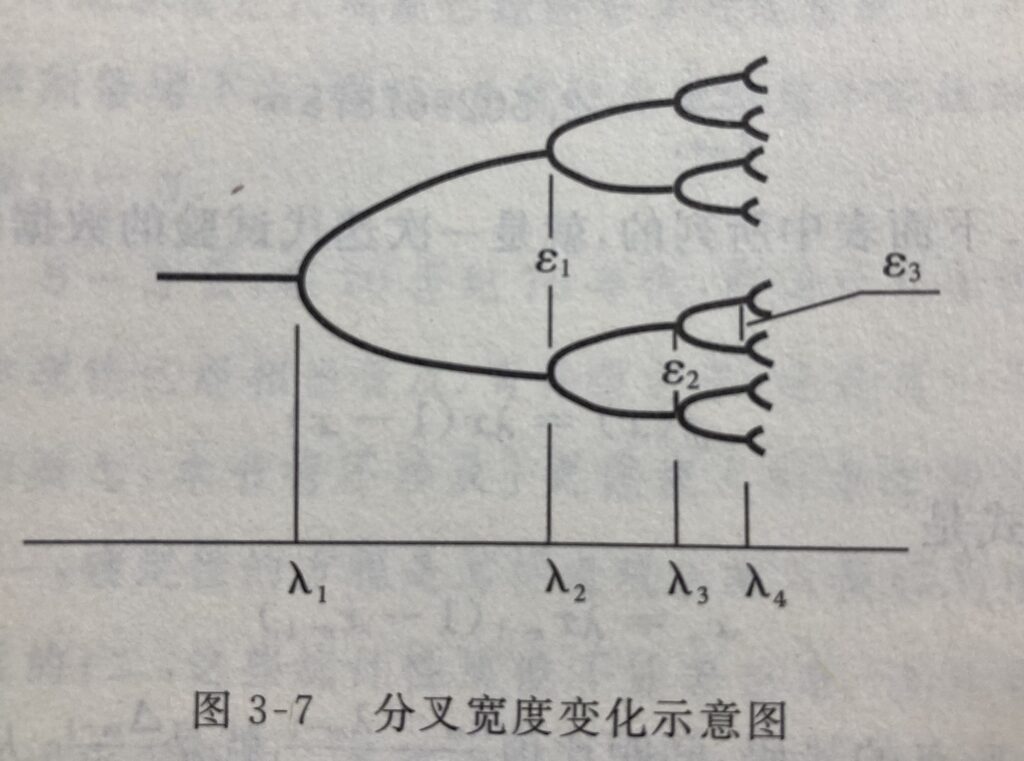
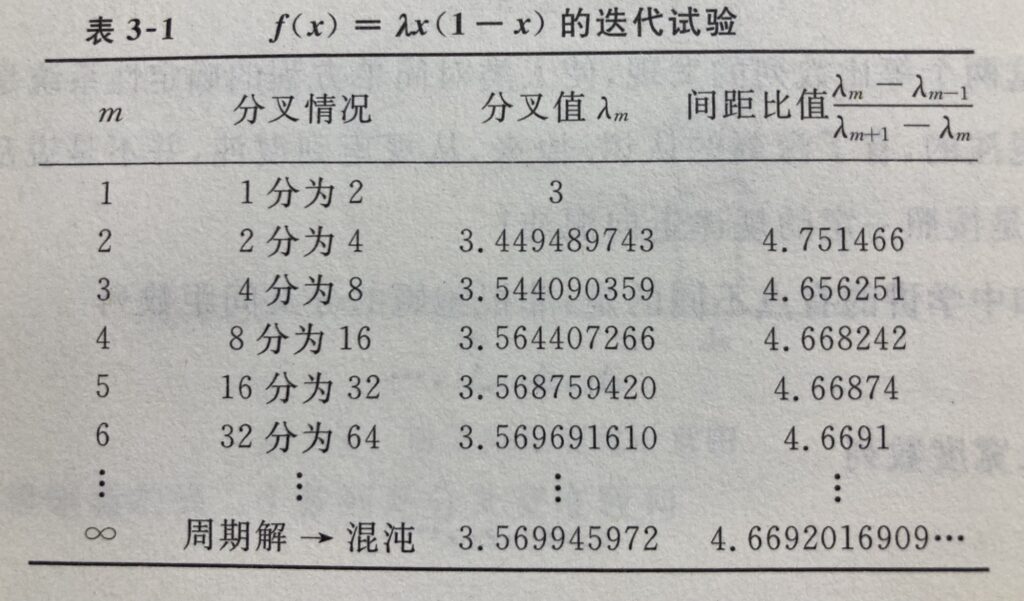
自然界普适常数——菲根鲍姆常数:
分叉间距之比趋向:δ=4.669201609…
分叉宽度之比趋向:a =2.502907875…
一个确定性的数学系统,只要具备产生混沌现象的条件(eg,区间迭代只要有一个3周期点或奇数周期点),就要提防这种不稳定的现象。这种不稳定现象,在数学里通常称为“对初值的依赖非常敏感”,初始值差一点点,后面差很多很多。
混沌现象一个很显著的直观特征就是它的不稳定性,“差之毫厘,谬以千里”。
世界上第一颗原子弹在洛斯阿拉莫斯实验室研制出来。
物理学中有确定性和概率性两套描述体系。牛顿力学,是确定性描述体系;分子物理学喝热力学是概率性描述体系。
确定性系统的假的随机过程,叫作伪随机过程,不是由数据的随机性产生的,而是由系统本身的内在随机性产生的,运行下去,一定会出现类似随机过程的混沌现象。所以,确定性描述喝概率性描述之间,并没有不可逾越的鸿沟。
随机过程是短期内久无法预测的现象,伪随机过程却是短期内可以预测、长期才不可预测的现象。
一般来说,混沌是比有序更为普遍的现象,就像无理数比有理数多得多一样。混沌理论的诞生被许多人认为是理论物理学的一个新的篇章的开始。
艺术应该是人类看待世界的方法论。
四 经济:一般经济均衡理论
有限纯交换经济的基本假设:m个商人交换n+1种商品。
n+1种商品,编号为第0种商品,第1种商品,……第n种商品。第0种数量x0,第一种x1,……第n种xn,合起来写得到商品向量X=(x0,x1,…xn)。
平面上建立直角坐标系后,平面上的每一个点可以用一对实数(x,y) 表示.我们把点和从坐标原点到这个点的向量看作一样东西所以平面上每一个向量由一对实数(x,y)组成,x叫作这个向量的第一个分量,y叫作这个向量的第二个分量,高中学解析几何的时候又知道,空间建立直角坐标系后,空间中的每一个点可以用一组三个实数(x,y,z)来表示.所以,(x,y,z)也就表示空间中的一个向量,它的第1个分量是x,第2个分量是y,第3个分量是z .
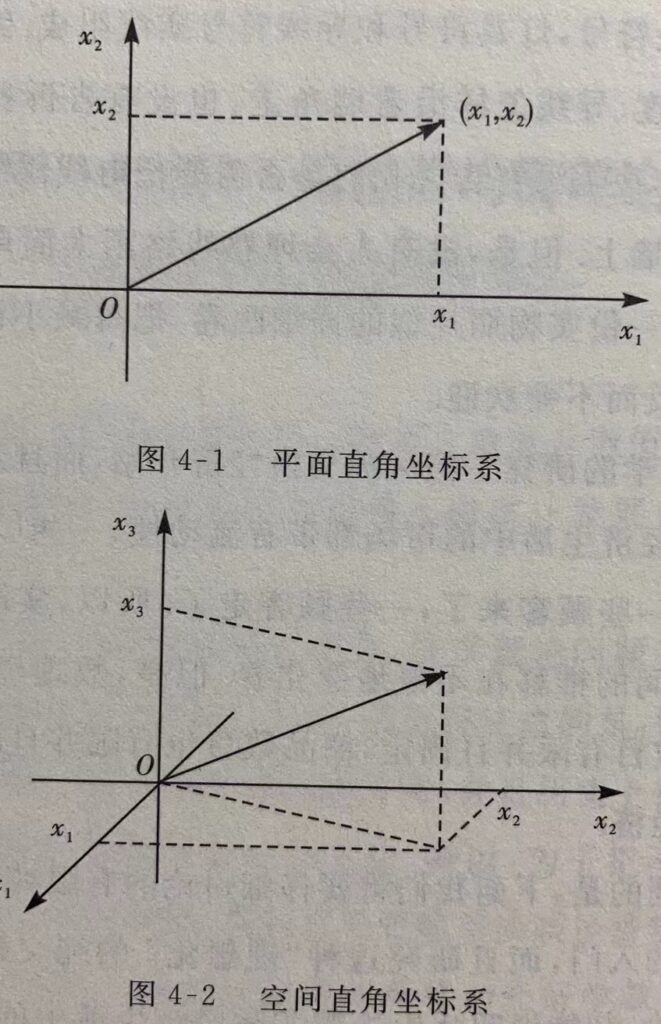
为了统一 , 把x和y写成x₁和x₂,把x,y,z写成 x1,x2,x3.所以,(x1,x₂)表示平面上的一个向量,(x1,x2,x3)表示空间中的一个向量.平面上的向量用2个实数分量x1和x₂表示,所以平面也叫作2维空间.原来说的空间中的向量用3个实数分量x1,x2,x3表示,所以平常我们说的空间也叫作3维空间.推而广之,数轴上的点和数轴上的从原点到这个点的向量只用1个实数表示,所以数轴是1维空间.
X=(x0,x1,…xn)叫作商品向量,叫作一个n+1维的商品向量。每个分量都不会是负数。
下标j表示第j种商品,Xj表示第j种商品数目,上标i表示第i个商人,Xi表示第i个商人的商品向量。
每个商人所拥有的各种商品就可以用一个n+1维商品向量来表示.这个向量的第j个分量是多少,就表示该商人有多少第j种商品.但每个商人在交换之前和交换之后所具有的商品在数目上是不同的.例如一个铁匠在交换前有10把锄头,交换后剩下两把锄头,但用8把锄头换来了40公斤面粉,12尺布.假如参与交换的只有这三种商品,那么这个铁匠在交换前的商品向量是(10,0,0),在交换后的商品向量是(2,40,12),可见是不同的.为了区别每个商人在交换前和交换后的商品向量,我们把交换前的商品向量用字母w表示,称为初始库存向量,交换以后的商品向量,还是用X表示.这样一来,wi=(wi0,wi1,…,win)就表示第i个商人初始(交换前)库存第0种商品的数目是 wi0,第1种商品的数目是wi1,…,第n种商品的数目是win.
现在,假如第0种商品的价格是p0,第1种商品的价格是p1,……第n种商品的价格是pn,我们又得到一个n+1维的价格向量P=(p0,p1,..,pn),价格向量也是所有分量都不是负数的向量.
有了价格向量以后,很容易算出第i个商人的财富有多少,因为第i个商人的初始库存向量是wi=(wi0,wi1,…,win),而价格向量是P=(p0,p1,…,pn),所以他的财富(按货币计算)是
bi=p0wi0+p1wi1+…+pnwin
纯交换经济一个基本假设:每个商人交换后所具有的商品的总值不超过交换前他据有的商品的总值——“花费不得超过财富”原则:第i个商人的经济活动必须符合不等式
p0xi0+p1xi1+…+pnxin ≤ p0wi0+p1wi1+…+pnwin = bi
纯交换经济,不增加社会财富。有经济学家认为偏好是一切经济活动(并不限于纯交换经济)的动机的真正内涵,货币或价值反倒是一种外部标志。偏好,在数理经济学纯交换经济模型中,用效用函数表示,3个商人交换5种商品,假设商人们的效用函数分别为:
π1=x0+4x1+ 0.5x2+7x3+3x4
π2=5x0+ 2x₂+1.2x3
π³= 2x0+120x1 +3x₂+4x3+0.3x4
只要价格向量确定,每个商人财富可算。虽然需要价格向量,却不必出现货币,而且价格向量(的每一个分量同时)乘一个正数,也不会影响交换结果。重要的是各种商品价格之比,而不是各种商品价格本身。把价格向量乘一个非零或除以一个非零数,使之变成各分量之和为1的作用完全一样的新的价格向量,这叫规范化处理。需求是否满足,要看整个纯交换经济中的总初始库存和总的需求向量是否平衡。
过需求商品向量:g=d-w,w库存,初始库存W;总的需求向量d。反应对商品j的供求关系,供不应求gj>0;供过于求gj<0 。库存和需求都用价格来计算,瓦尔拉斯法则:p0g0+……+pngn=0
纯交换经济假设之下,存在一种每个商人都达到最优的格局。帕累托最优,不仅对整体最优,对每个商人来说,也甘愿接受的最优。
不动点定理:
好吧,真是看不下去了。



